Teletransporte

Introducción

En el presente informe se tratará un aspecto de la mecánica cuántica que es tan actual como sorprendente. Se trata de la posibilidad de teletransportar una partícula (como podría ser un fotón) de un sitio a otro lejano, y si bien ya en la década del 30 comenzaron a gestarse las bases para esta idea, el tema de estudio tiene su máximo desarrollo en los últimos diez años.

El teletransporte consiste en “traspasar” el estado cuántico de una partícula a otra a gran distancia (lo que equivale, objeciones mediante, a teletransportar la partícula misma). Para ello previamente las partes intervinientes (por ejemplo dos fotones que llamaremos 1 y 2) deberán entrelazarse, estado conocido como EPR. Dichas partículas podrán alejarse, supongamos, una a cada lado del universo (lo que en el laboratorio serían centímetros ó metros de distancia). Posterior a esto, se toma una de las partículas (fotón 1) y se la entrelaza con otra (que llamaremos fotón X) cuyo estado cuántico es totalmente desconocido y se desea teletransportar. Este entrelazamiento, y la posterior medición del estado de Bell de dicho par (fotones 1 y X), hacen colapsar a la partícula que se encuentra alejada (fotón 2) en un estado cuántico definido. Operación mediante, la partícula alejada (fotón 2) deviene en el mismo estado que el de la partícula que se teletransportó (fotón X).
Cómo ocurre ese “viaje” del estado cuántico de la partícula es aún desconocido. Sin embargo, esta potencial posibilidad que brinda la cuántica se intenta aplicar a cosas concretas, por ejemplo el desarrollo de computadoras atómicas.

Si bien es oscuro el panorama respecto a si existe ó no transferencia de información entre partículas de un par entrelazado alejadas grandes distancias, en este informe se desarrollan los conceptos teóricos fundamentales del tema, como así también se brinda una explicación detallada del protocolo que permite llevar a cabo el teletransporte de información cuántica.

La paradoja EPR y el teorema de Bell

Según el Principio de Incertidumbre establecido por Werner Heisenberg en 1927 no es posible tener conocimiento preciso y al mismo tiempo de ciertos pares de magnitudes que definen al estado cuántico de una partícula (conocidas como “magnitudes conjugadas”). Un ejemplo claro lo constituyen la posición y la cantidad de movimiento. Si midiésemos con precisión la primera, no tendríamos en absoluto información sobre la segunda, y viceversa.

Sin embargo, en el año 1935, los científicos Albert Einstein, Boris Podolski y Nathan Rosen publicaron un documento titulado “Can the Quantum Mechanical Description of Reality be Considered Complete?”, en el cual proponían la posibilidad de violar el Principio de Incertidumbre. Para ello imaginemos dos partículas (digamos fotones) a las cuales se les permite interactuar. Así el sistema queda descrito por una única ecuación de onda de Schrodinger (lo que se conoce como entrelazamiento). Posteriormente los fotones son separados, pero continúan siendo representados por una única ecuación de onda. Entonces la medición de alguna de las magnitudes de uno de los fotones inmediatamente brinda información acerca de la misma magnitud pero del otro fotón. Por ejemplo, decir que el fotón 1 tiene spin en el eje x de +½ es suficiente para saber que el fotón 2 tendrá un spin en el eje x de – ½, pero sin haber efectuado medición alguna sobre este último. Es así como surge la Paradoja EPR (Einstein, Podolsky, Rosen), según la cual se podría medir una magnitud (digamos posición) en uno de los fotones, y otra magnitud (digamos momentum) en el otro fotón, pero de acuerdo a la correlación anteriormente descripta se dispondría de ambas magnitudes para ambos fotones, y es justamente ésta posibilidad la que es vedada por el Principio de Incertidumbre.

La mecánica cuántica intentó por varios años dar una explicación a la paradoja EPR. Pensando a los fotones anteriores como constituyentes de un mismo sistema y representados por una misma ecuación de onda, podemos decir que cualquier medición sobre el fotón 1 “colapsa” el estado cuántico del otro, igual que si la medición se hubiese llevado a cabo en el fotón 2. Entonces, sin importar la distancia que los separe, ambos fotones disponen de algún tipo de relación tal que, midiendo el estado en uno de ellos, queda inmediatamente definido el estado del otro integrante del par. Se dice, pues, que las partículas (en este caso fotones) están en un estado EPR.
Esta explicación que ofrece la mecánica cuántica clásica se fundamenta en una teoría conocida como Principio de No Localidad, según el cual el comportamiento de la naturaleza es no local, y, en el caso de los fotones, la medición sobre uno de ellos tiene efectos inmediatos en el otro (independientemente de la distancia que los separe). Esto implica que, previamente a cualquier medición, las partículas no tienen estados cuánticos definidos, sino una combinación de todos los estados posibles. No existe una realidad cuántica hasta que el observador efectúa la medición correspondiente. En ese sentido, y desde el punto de vista clásico, un sistema cuántico es no local y dependiente del observador.

La posibilidad que brinda la mecánica cuántica de que la naturaleza sea no local e irreal no era completamente aceptada por Einstein, Podolsky y Rosen. Según ellos podemos suponer la existencia de variables ocultas; esto es, información propia de cada partícula, y que surge en el momento en que ambas interactúan, para después ser separadas. Es decir, el estado EPR ó de entrelazamiento consiste, según este punto de vista, en una serie de instrucciones que portan cada una de las partículas, y que en cierta forma son sincronizadas al momento de la interacción. Con esta visión, EPR sostenían que no había ningún tipo de transferencia a distancia, y que, por consiguiente, no se violaba la Teoría de la Relatividad (y el límite impuesto de la velocidad de la luz). Esta claro que esta concepción es puramente local, y asume que existe una realidad previa a la medición, es decir, independiente del observador.
Aceptando la existencia de variables ocultas, EPR tildaron a la mecánica cuántica como incompleta, ya que no brinda los medios necesarios para conocer dicha información subcuántica.

Hasta aquí tenemos dos ideas que intentan explicar el mismo fenómeno: una naturaleza no local según la mecánica cuántica, ó la existencia de variables ocultas según EPR.
Un principio de solución a dicho dilema deviene en el año 1964, cuando el físico británico John Stewart Bell establece el teorema y la desigualdad que llevan su nombre. Bell asume la existencia de variables ocultas, y de una naturaleza local, al mejor estilo EPR. Con estas hipótesis construye una relación matemática conocida como desigualdad de Bell. De ser probada, dicha relación confirmaría las ideas de EPR; de lo contrario estaríamos frente a un universo no local y, además, dependiente del observador.
Por entonces no estaban dadas las condiciones tecnológicas para poder probar experimentalmente la desigualdad de Bell, con lo cual debió esperarse a principios de los 80. Más precisamente en 1982, un grupo de científicos franceses, liderados por Alain Aspect, demostraron en laboratorio que la desigualdad de Bell era violada, confirmando el concepto de no localidad.
Si bien todas las experiencias han sufrido algún tipo de objeción, en reiteradas oportunidades los resultados han sido contundentes. Esto es, que se viole la desigualdad de Bell significa que todo par de partículas en un estado EPR se encuentran de alguna forma entrelazadas a nivel cuántico de manera tal que cualquier medición sobre una de ellas equivale a medir el estado de la otra partícula de dicho par.

De acuerdo a lo antes dicho, un par de partículas, por ejemplo fotones, pueden constituirse en un estado de correlación. Esta correlación permite que los integrantes del par interactúen por más distanciados que se encuentren. Es a este tipo de estados a los que se los llama “entrelazados” (entanglement), y será en base a esta posibilidad de “interacción a distancia” que desarrollaremos el concepto de teletransporte de partículas.

Teletransporte de un estado cuántico desconocido

Vamos a citar un ejemplo claro que permite comprender qué significa teletransportar partículas (ó, más precisamente, estados de partículas). Supongamos que una persona dispone de un par de dados. Bate el cubilete y tira: salen dos 6. Bate nuevamente y vuelve a tirar: ahora son dos 1. Una vez más tira, y salen dos 4. Así sigue arrojando sus dados una y otra vez, y siempre la misma situación: ambos dados muestran la misma cara (ó sea, el mismo número). Sabiendo que los dados no están trucados ó cargados, podría pensarse que existe algún tipo de relación entre ellos que produce dicho fenómeno. Una situación similar se da cuando dos partículas se encuentran entrelazadas. Cada una de ellas posee un conjunto de propiedades cuánticas que tienen relación con las propiedades de la otra partícula. El entrelazamiento es el principal actor de esta historia, ya que, de acuerdo al principio de no localidad, dos partículas están vinculadas a distancias muy grandes, y eso tiene sus ventajas.

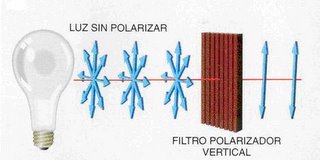
Qué información en particular vamos a teletransportar es irrelevante, siempre y cuando tomemos magnitudes cuánticas que representen el estado de una partícula entrelazada con otra. En lo que sigue haremos referencia a la polarización de fotones, y transferiremos esta característica entre el par entrelazado. Según las ecuaciones de Maxwell, el campo electromagnético en el vacío se compone de un campo eléctrico E y de un campo magnético B, perpendiculares entre si, y ambos perpendiculares a la dirección de desplazamiento c del campo electromagnético (ver Figura 1)


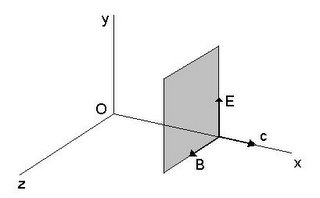
La polarización es la manera en que se alinean las oscilaciones del campo eléctrico, y, si bien es plausible de adoptar diferentes valores, nosotros vamos a considerar a efectos prácticos sólo dos de ellos: horizontal ó vertical.

Llamemos Alice a la persona que envía el mensaje teletransportado, y Bob a quien lo recibe (ver Figura 2). En primer lugar, tanto Alice como Bob deben poseer uno de los fotones del par entrelazado (fotón A para Alice, y fotón B para Bob). El mensaje cuántico a enviar consiste en el estado de polarización de un tercer fotón en manos de Alice (fotón C). Dicha polarización es desconocida por Alice, y debe serlo si es que nos queremos ajustar al Principio de Incertidumbre. En todo caso, si intentamos medir dicha polarización, y en base a ese principio, el resultado no es exactamente el que posee el fotón en sí (hay una incertidumbre en la medición).
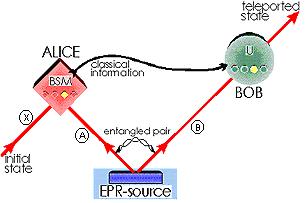
El próximo paso consiste en entrelazar los fotones A y C, ambos en poder de Alice. ¿Cuál es el objetivo de entrelazar a los fotones A y C? La idea es que si no se puede conocer el estado absoluto del fotón C (por lo explicado anteriormente), sí se puede conocer el estado relativo de dicho fotón respecto al fotón A. Esto es, no podemos decir que C tiene polarización vertical ó polarización horizontal del campo eléctrico, pero sí es posible brindar información del estado de dicha polarización respecto de la del fotón A. Esta correlación da lugar a un nuevo estado entre ambos, comúnmente llamado estado de Bell. Las posibilidades de correlación son cuatro, ya que tanto el fotón A como el fotón C pueden tener, como ya mencionamos, polarización vertical u horizontal. La notación matemática de los estados del Bell puede verse en la Figura 3.
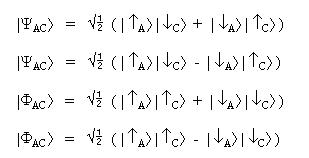Como puede verse, cada estado de Bell no es otra cosa que una combinación lineal de los posibles estados de cada fotón por separado. La ventaja es que es posible conocer el estado de Bell de un par entrelazado, mediante el uso de dispositivos adecuados.

Una vez que Alice ha determinado cual de los cuatro posibles estados de Bell presenta su par de fotones A y C, queda inmediatamente correlacionado el fotón B de Bob con el par A-C de Alice. Esto significa que el fotón B dispone ya de la información suficiente para transformarse en el fotón C. En el mejor de los casos, el fotón de Bob es igual al fotón C. En las otras tres posibilidades (de acuerdo al resultado de la medición de Alice), Bob deberá aplicar algún tipo de operación sencilla sobre su fotón, como ser rotaciones de 180° de la polarización en torno a alguno de los ejes X, Y ó Z. En todos los casos, el resultado es que el fotón B adquiere el mismo estado cuántico que el fotón C (el cual se deseaba teletransportar). Pero lo más interesante es el hecho de que el fotón C “desaparece” de las manos de Alice. Una vez que dicho fotón fue entrelazado con el A, pierde toda información particular. Esto confirma la no violación del Principio de No Clonación. Dicho principio establece que, a diferencia de la información clásica, los estados cuánticos no pueden duplicarse. En nuestro caso no podrían haber dos fotones C.

Sin embargo, la transmisión de la información tiene ciertas restricciones relativistas. Si bien la correlación entre el par de fotones A-C de Alice y el fotón B correspondiente a Bob es “instantánea”, se necesita de algún medio clásico de manera tal que Alice pueda comunicarle a Bob que ya ha realizado la medición pertinente y que el resultado es tal ó cual estado de Bell. Cualquier forma de comunicación que desee utilizar Alice para informarle a Bob de sus resultados estará restringida a no sobrepasar la velocidad de la luz (por ejemplo una llamada telefónica, señales radioeléctricas, etc.).
Tenemos, pues, dos canales a través de los cuales se comunican Alice y Bob: un canal cuántico, dado por el estado EPR de los fotones A y B, y un canal clásico (cualquier forma de comunicación hasta hoy conocida, sujeta a condiciones relativistas).
Supongamos ahora que deseamos eludir el uso de dicho canal clásico de comunicación. Bob podría, por ejemplo, tratar de adivinar cual de los cuatro estados de Bell ha medido Alice, y así aplicar la operación correcta sobre su fotón B. Tendremos entonces que Bob se equivoca un 75% de las veces, y ni siquiera en el otro 25% tendrá la certeza de haber acertado. En definitiva su fotón B es tan aleatorio como cualquier otro, más allá de que Alice ya haya efectuado su medición.

El procedimiento anterior adoptado tanto por Alice como por Bob constituye una suerte de protocolo para llevar a cabo el teletransporte. Algunas consideraciones a tener en cuenta son, por ejemplo, que Alice y Bob pueden estar a centímetros, metros ó años luz de distancia, y sin embargo el fenómeno continuaría produciéndose. También es interesante destacar que no se viola el principio de incertidumbre, ya que Alice mide el estado de Bell de los fotones A y C entrelazados, pero no de cada uno por separado. En definitiva se está teletransportando un estado cuántico desconocido tanto por Alice como por Bob, el estado del fotón C.
Sin embargo, en teoría todo pareciera estar fundamentado. Pero ¿qué sucede en la realidad? ¿Se han llevado a cado experimentos en laboratorio que confirmen los resultados teóricos anteriores? A continuación analizaremos este tema, en base a una experiencia conducida por el físico Anton Zeilinger, de la Universidad de Innsbruck, Viena, junto a sus colaboradores.



Construyendo un teletransportador : el experimento de Zeilinger

En el año 1997, el físico Anton Zeilinger, junto con sus colaboradores, de la Universidad de Innsbruck, construyeron un dispositivo capaz de teletransportar el estado cuántico de un fotón entre dos lugares diferentes dentro del laboratorio.


Para ello, un impulso de luz ultravioleta atraviesa un cristal produciendo dos rayos de luz (llamados A y B), cuyos fotones están entrelazados (ver Figura 5). Uno de estos rayos (el haz A) estará en manos de Alice, mientras que el otro rayo (el haz B) corresponderá a Bob.


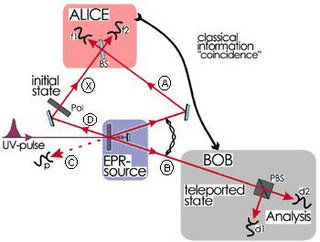
Así, ambos tendrán en su poder fotones entrelazados. Un tercer rayo de luz ultravioleta es nuevamente reflejado, volviendo a atravesar el cristal, y generando, por consiguiente, dos nuevos haces de fotones entrelazados (llamados ahora C y D). El haz de luz C simplemente “muere” en un detector, y se utiliza como aviso de que ya está listo el haz de luz D. Los haces C y D están entrelazados, sin embargo no nos interesa esta particularidad. Más aún, el haz de luz D es polarizado en alguna orientación posible, pasando a llamarse X (ver Figura 6), y es a partir de entonces que ya disponemos de un haz a teletransportar. Se teletransportará el estado cuántico de los fotones del rayo X, que, previa polarización, perdió todo tipo de correlación ó entrelazamiento con el haz C.
Hasta aquí Alice cuenta con dos haces de luz ultravioleta: los rayos A y X. Por su parte, Bob dispone del haz B, entrelazado con el haz A de Alice.

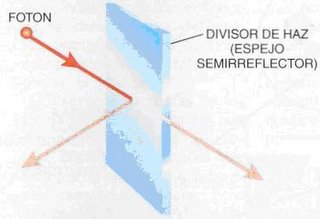
Concentrémonos en Alice, y en las operaciones a llevar a cabo sobre los fotones de los haces A y X. De acuerdo a lo desarrollado anteriormente, tanto los fotones del haz X como los del haz A deberán entrelazarse. Esto es, ambos pasarán a un estado correlacionado en donde “pierden” sus características cuánticas individuales para adquirir propiedades en conjunto, es decir, un estado de Bell. Cada uno de los haces entrelazados desconoce si la polarización de sus fotones es vertical u horizontal, ahora sólo sabrá cómo está orientada su polarización respecto a la del otro fotón. Una correlación de este tipo puede lograrse, en líneas muy generales, haciendo uso de un dispositivo conocido como divisor de haces. Se trata de un espejo semirreflector capaz de reflejar el 50% y transmitir el otro 50% del haz de luz que se proyecta en una de sus caras (ver Figura 7).

Para lograr la correlación basta con hacer incidir los haces A y X sobre caras opuestas del espejo semirreflector (ver Figura 8), dando lugar a cuatro posibilidades. Estas son:

Que ambos haces se reflejen (yendo a parar a detectores diferentes).
Que ambos haces se transmitan (yendo a para a detectores diferentes).
Que el haz X se refleje y el haz A se transmita (yendo a parar al mismo detector).
Que el haz X se transmita y el haz A se refleje (yendo a parar al mismo detector).

Un aspecto problemático estriba en las cuatro posibilidades anteriores: si ambos haces van a parar al mismo detector (es decir, que uno se transmita y el otro se refleje) permite conocer con precisión cuál de los haces fue transmitido y cuál fue reflejado, situación vedada por el principio de incertidumbre. Sólo se nos está permitido medir la propiedad relativa, que se da cuando ambos haces van a parar a detectores diferentes, o sea, un 25% de las veces. En el caso que Alicie mide fotones en detectores diferentes es que se produce el teletransporte. Así, el haz de luz B que está en poder de Bob pierde su estado individual para convertirse cuánticamente en el haz X que Alice deseaba teletransportar. Aún resta, para completar el teletransporte, que Alice le informe a Bob el resultado de su medición del estado de Bell de los haces A y X, haciendo uso de algún medio clásico de comunicación. En realidad, sólo un 25% de las veces el experimento tiene éxito, ya que el entrelazamiento de A y X se produce cuando ambos haces van a detectores diferentes.
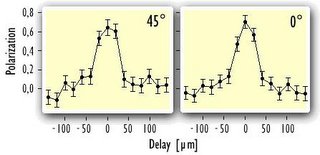
Una vez concretado el teletransporte, el equipo de investigadores de Innsbruck chequeaba el estado cuántico del haz de luz X, ahora en manos de Bob. Los resultados fueron alentadores: la polarización correcta fue detectada aproximadamente un 80% de las veces. Sin embargo el experimento no es perfecto. La Figura 9 muestra los resultados de la polarización del fotón B (a 0° y 45°) en función del delay entre la llegada de los fotones A y X al divisor de haces de Alice. En esos gráficos puede observarse que el máximo de éxitos se encuentra alrededor del cero, es decir, cuando los fotones A y X llegan simultáneamente al divisor de haces. En particular, la probabilidad de que el teletransporte se concrete exitosamente es de un 70% + - 3%, según los análisis realizados por el equipo de científicos.

Varias experiencias fueron llevadas a cabo al respecto. Tal vez la de Innsbruck sea una de las más reconocidas. Sin embargo, en 1998, el grupo de Jeffrey Kimble del Instituto de Tecnología de California (CALTECH) logró teletransportar un estado cuántico de un haz de luz a otro, confirmándose así la posibilidad del teletransporte de un aspecto continuo.

Conclusiones

Si bien el desarrollo experimental del teletransporte es aún limitado, todo indica que el futuro del tema es sorprendentemente amplio. Las aplicaciones son muchas e importantes, como ser la construcción de computadoras cuánticas. Dentro de dicho campo de aplicación, la comunicación entre ordenadores ya no requeriría de cableado (las hoy conocidas ‘redes de computadoras’), y ni hablar de los tiempos de transferencia. ¡Todo ocurriría instantáneamente!

También están quienes sostienen que el teletransporte de objetos de mayor tamaño (por ejemplo moléculas), e incluso de seres vivos (como pudiese ser un virus) es una posibilidad concreta a largo plazo. Claro está que no es tarea fácil, ya que en esos casos se necesitaría entrelazar las moléculas. Además, a medida que los cuerpos son más grandes en tamaño, surge un nuevo inconveniente: la decoherencia. Esto es, cualquier interacción del cuerpo a teletransportar con el medio exterior produce el fracaso del procedimiento.

Claro está que, más allá de ser implementado a largo plazo, el teletransporte se construye sobre bases teóricas muy fuertes. Hay, por lo menos, 75 años de historia en el campo de la cuántica, durante los cuales se han ido construyendo los cimientos que, hoy en día, permiten, al menos, concretar el teletransporte de fotones dentro del laboratorio. Estamos viviendo una etapa de transición, que nos conducirá lentamente a resultados más alentadores. Y quién sabe si dentro de 100 ó 150 años todo aquello que pertenecía al mundo de la ciencia ficción no llegará a ser una realidad.
Bibliografía


[1] Anton Zeilinger; Teletransporte Cuántico; Investigación y Ciencia; edición española de Scientific American; Número 285; Junio de 2000; páginas 58 a 67.

[2] Charles Bennett, Gilles Brassard, Claude Crépeau, Richard Jozsa, Asher Peres y William Wootters; Teleporting an Unknow Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels; Physical Review Letters; Número 13; Volumen 70; 29 de Marzo de 1993.

[3] Yoon-Ho-Kim, Sergei Kulik y Yanhua Shih; Quantum Teleportation with a Complete Bell State Measurement; 11 de Octubre de 2000.

[4] X. Yi, G. Jin y D. Zhou; Creating Bell states and decoherence effects in quantum dots system; 20 de Noviembre de 2000.

[5] Igor Volovich; Bell’s Theorem and Locality in Space; 1 de Diciembre de 2000.

[6] Quantum Mechanics; Enciclopedia Británica.

[7] Carlton Caves; A Tale of Two Cities; Science; Volumen 282; 23 de Octubre de 1998; páginas 637 a 638.

[8] A. Furusawa, J. Sorensen, S. Braunstein, C. Fuchs, H. Kimble y E. Polzik; Unconditional Quantum Teleportation; Volumen 282; 23 de Octubre de 1998; páginas 706 a 709.

[9] A. Einstein, B. Podolsky y N. Rosen; Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?; Physical Review Letters; 47, 777-780; 1935.

Autores

Browarnik, Gabriela
Brugues, Javier
Petrina, Sebastián
Schmidt, Gustavo
Vega, Augusto